Probability and Statistics for AI and ML Part-3

Statistics an introduction

The English word statistics is derived from the Latin word status or Greek word statista or perhaps from the German word statistik each of which means a political state. During ancient times governments used to collect data about their people’s population and wealth. The former to know the manpower availability to plan the State’s defence against external aggression, and the latter to plan taxes and levies from citizens.

Webster’s dictionary had defined Statistics as: “classified facts representing the conditions of the people in a State ...especially those facts which can be stated in numbers or in any other tabular or classified arrangements”.

Merriam-Webster’s dictionary in 2020 defines Statistics as: “a branch of mathematics dealing with the collection, analysis, interpretation and presentation of masses of numerical data”.

As a result of analysis and interpretation with statistical techniques we can draw valid inferences from data related to various sources such as businesses, education, demography, biology, healthcare, economics, psychology, politics, industry, agriculture, astronomy etc. Statistical analysis is indispensable for planning. 

Figure-1: A sample of uses of statistics

Statistics and Mathematics

Some consider statistics to be a distinct mathematical science rather than a branch of mathematics. While many scientific investigations make use of data, statistics is mainly concerned with the use of data and making decisions in the midst of uncertainty. According to L. R.Connor  “Statistics is a branch of applied mathematics which specializes in data” ^[1]. Statistics is essentially the application of mathematical theories and principles to real-world data.

This distinction will perhaps become clearer if we trace the thought process of two persons encountering their first six-sided dice game as described below.

Consider two mathematicians A and B who are friends, visiting a casino. Person A is an expert in Probability and B a statistician. Both observe a six-sided dice game. Person A calculates the probability of dice to land on each face as 1/6 and will figure out the chances of quitting the game. Person B would watch the game for a while to find out whether the dice is biased or unbiased and make sure that the observations are consistent with the assumption of equal-probability faces. Once confident enough that the dice is fair, B would call A for an opinion and apply probability to win the game.

Statistics is associated with applied mathematics and is concerned with the collection, analysis, interpretation, presentation, and organization of data. Statistical conclusions are true in terms of averages and hence are meant to be used by experts. Unlike the laws of physical and natural sciences, statistical laws are approximations and not exact. Prof W.I. King states that “Science of Statistics is the most useful servant but only of great value to those who understand its proper value”.

Why do we analyze data?

Data is essentially information collected from the population. Data analysis is the process of bringing order and structure to a mass of collected data in order to summarize it. Data Analysis is an attempt by a researcher to summarize collected data and helps to make decisions. To cite a few examples, Amazon and Google analyze data to implement recommendation engines, Page Ranking and demand forecasting, etc.

Analysis, irrespective of whether the data is qualitative or quantitative, will include

• Description of data and summarization.
• Comparison of variables, identification of differences and relationships between variables. 
• Forecast outcomes

After summarization data can be visualized using tables, bar charts, pie charts, graphs etc.  Labels, source names, foot notes, etc can be used to summarize data. Visualization of data is necessary to speed up decision making process and to take maximize decision accuracy.

Types of Data, Feature values in statistics

A data or feature value may take values from a continuous valued set (subset of R) or from a finite discrete valued set. If the finite discrete set has only two elements {0,1}, then the feature is binary valued or dichotomous. A different categorization of the features is based on the relative significance of the values they take. There are four categories of feature values:

1. nominal,
2. ordinal,
3. interval-scaled, and
4. ratio-scaled.

Nominal or unordered: This includes features whose possible values code states. Examples: a feature value that corresponds to male/female labels which can be represented numerically with 1 for a male and 0 for a female or vice-versa or colour names etc. Any quantitative comparison between these values is meaningless.  Operations valid are  =, ≠.

Figure -2 Nominal data

Ordinal: This includes features whose values can be meaningfully ordered. The Likert scale is an example of ordinal data. Another example: a feature that characterizes the performance of a student. Its possible values are 5, 4, 3, 2, 1 and that these correspond to the ratings “excellent”, “very good”, “good”, “satisfactory”, “unsatisfactory”. These values are arranged in a meaningful order. Other examples where order is meaningful are temporal and spatial sequences patterns such as events in telecommunication networks, sensor networks signal in a process plant, video, audio signals etc. Sequence of activities by a web site visitor, activities in industrial organization, conduct of academic course, etc can have temporally ordinal relations. Spatial order is a method of organization in which details are presented as they are (or were) located in space. Speeches for example that focus on processes or demonstrations use a chronological speech pattern as well. For ordinal sequences the difference between two successive values is of no meaningful quantitative importance. Both nominal and ordinal are a finite set of discrete values. Operations valid for ordinal variables are =, ≠, >, <, ≤, ≥.

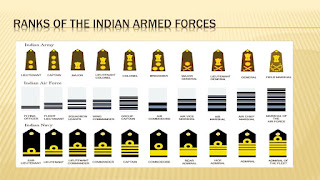
Figure-3: Ordinal Data

Interval-scaled: If, for a specific feature, the difference between two values is meaningful while their ratio is meaningless, then it is an interval-scaled feature. Example: the measure of temperature in degrees Celsius. If the temperatures in N. Delhi and Kochi are 15 and 30 degrees Celsius respectively, then it is meaningful to say that the temperature in Kochi is 15 degrees higher than that in Delhi. However, it is meaningless to say that Kochi is twice as hot as N. Delhi. Operations valid for interval scaled variables =, ≠, >, <, ≤, ≥, +, −.

Figure-4: Interval Scaled Data

Ratio-scaled: If the ratio between two values of a specific feature is meaningful, then this is a ratio-scaled feature. Example of such a feature is weight, since it is meaningful to say that a person who weighs 100 kg is twice as fat as a person whose weight is 50 kg. Operations valid for interval scaled variables =, ≠, >, <, ≤, ≥, +, −, ×, ÷.

Figure-5: Ratio Scaled Data

NOIR levels

By ordering the types of features as nominal, ordinal, interval-scaled, and ratio scaled, one can easily notice that each subsequent feature type possesses all the properties of the previous types. For example, an interval-scaled feature has all the properties of the ordinal and nominal types.

Figure-6:  NOIR attributes

Classification of data types: Data and features can be quantitative or qualitative.

(1) Quantitative feature variable: e.g., 

• continuous valued (e.g., weight, mass etc);
• discrete valued (e.g., the number of computers);
• interval valued (e.g., the duration of an event).

Quantitative features can be measured on a ratio scale with a meaningful reference value, (such as temperature), or on interval, ordinal or nominal scales.

(2) Qualitative feature variables:

• nominal or unordered (e.g., color, labels, names, phonemes etc); 
• ordinal (e.g., military rank or qualitative evaluations of temperature (“cool” or “hot”) or sound intensity (“quiet” or “loud”)).

Dependent and Independent Variables

An independent variable, which sometimes is also called an experimental or predictor variable, is a variable that is being manipulated in an experiment in order to observe the effect on a dependent variable, which is sometimes also called an outcome variable.

As a simple example, consider a student’s performance score variable which is outcome of an experiment. The score could be dependent on two independent variables which are time duration measured as hours of study and intelligence measured using IQ score.

Descriptive and Inferential Statistics

The field of statistics can be broadly divided into descriptive statistics and inferential statistics. Both are essential for scientific analysis of data. AI/ML engineers and data scientists will need high level understanding of both and the common statistical methods which are decision support tools to be able to derive conclusions from statistical studies.

Figure-7: Descriptive and Inferential statistics

Descriptive Statistics

Descriptive statistics describes data or provide summarized details about a whole group data or population data, through numerical calculations, graphs or tables etc. A population data set contains features and characteristics of all members in the group. For example, we could calculate the mean and standard deviation of the exam marks for 100 students. The 100 students would represent your population. A population can be small or large, as long as it includes all the data you are interested in.  Descriptive statistics methods are applied to populations, and the properties of populations which are called parameters as they represent the whole.

Common Descriptive statisticsMeasures  of frequency:  

• Count, Percent, Frequency.
• Measures of position: Quartile ranks, Quantile ranks, Percentile ranks.
• Measures of Central Tendency: Mean, Median, Mode.
• Measures of Dispersion or Variations: Range, Interquartile range, Standard Deviation, Variance, Measures of shape: Skewness and Kurtosis

Figure-8: Descriptive Statistics

Inferential Statistics

When access to the whole population you are interested in investigating is impossible, and if access is limited to a subset of the population we make use of a sample that represents the larger population. Inferential statistics draws conclusion about the larger population by examining samples of collected data and make predictions about the population.

Figure-9: Inferential Statistics

For example, you might be interested in the marks obtained by all engineering students in Kerala. If it is not feasible to collect the student marks in whole of Kerala you can gather samples from a smaller set of students  and use it to represent the larger population. Properties of samples, such as the mean or standard deviation, are not called parameters, but they are called statistics.

Figure-10:  Sampling the population to estimate the parameter

From the above figure it can be understood that sample sets are drawn from the populations to estimate the mean. In the above figure 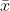 is a sample estimate of the true mean of a population characteristic. It is called a statistic.

Inferential statistics

Inferential statistics include the mathematical and logical techniques to make generalizations about population characteristics from sampled data. Inferential statistics  can be broadly categorized into two types: parametric and nonparametric. The selection of type depends on the nature of the data and the purpose of the analysis. 

Parametric inferential statistics involves 1) Estimation of population parameters, 2) Hypothesis testing

Fundamentally, all inferential statistics procedures are the same as they seek to determine if the observed (sample) characteristics are sufficiently deviant from the null hypothesis to justify rejecting it.

Figure-11: Flow chart of inferential statistics

There are many steps to do inferential statistics. Procedure for Performing an Inferential Test:

1. Start with a theory
2. Make a research hypothesis
3. Determine the variables
4. Identify the population to which the study results should apply
5. Set up the null hypothesis and alternate hypothesis
6. Choose the appropriate significance level
7. Collect sample sets from the population
8. Compute the sample test statistics or criteria that characterize the population
9. Use statistical tests to see if the computed sample characteristics are sufficiently different from what would be expected under the null hypothesis to be able to reject the null hypothesis.

Estimation of population parameters and sampling:

These population characteristics are measures of central tendency, spread or dispersion, shape, and relationship between independent (causal) and dependent (effect) data variables. It is, therefore, important that the sample accurately represents the population to reduce error in conclusions and predictions. The choice of sample size, sampling method and variability of samples can influence accuracy of predictions. Inferential statistics occur when there is sampling and arise out of the fact that sampling naturally incurs sampling error and thus a sample is not expected to perfectly represent the population. Confidence intervals are a tool used in inferential statistics to estimate a parameter (often the mean) of an entire population.

Hypothesis testing:

The second method of inferential statistics is hypothesis testing. Inferential statistics is strongly associated with the mathematics and logic of hypothesis testing. Hypothesis testing involves estimation of population parameters and the researcher’s belief about population parameters. Often, this involves comparison of means by analysis of variances two or more independent data groups. This method is called the analysis of variance (ANOVA). Such tests are often used by pharmaceutical companies that wish to learn if a new drug is more effective at combating a particular disease than using another existing drug or no drug at all. 

A hypothesis is an empirically (experimentally) verifiable declarative statement concerning the relationship between independent and dependent variables and their corresponding measures. The basic concept of hypothesis is in the form of an assertion, which can be experimentally tested and verified by researchers. The main goal of the researcher is to verify whether the asserted hypothesis is true or whether it can be replaced by alternate one. Therefore hypothesis testing is an inferential procedure that uses sample data to evaluate the credibility of a hypothesis about a population.

The default assumption is that the assertion is true. As examples consider these two hypotheses

1. Drug A and Drug B has the same effect on patients.
2. There is no difference between the mean values of two populations.

These are called the null hypotheses H₀. The counter assumption is the null hypothesis is not true. This is called the alternate hypothesis H_A.

Data collected allows the researcher, data analysts or statistician to decide whether the null hypothesis can be rejected and the alternate one can be accepted and if so, with what confidence measure?

A statistical test procedure is comparable to a criminal trial; a defendant is considered not guilty as long as guilt is not proven. The prosecutor tries to prove the guilt of the defendant. Only when there is enough charging evidence, the defendant is convicted.

In the start of the procedure, there are two hypotheses 

H₀: "The defendant is not guilty", and 

H_A: "The defendant is guilty".

The null hypothesis,  is the hypothesis the research hopes to prove and will not accepted until it satisfies the significance criterion. The test for deciding between the null hypothesis and the alternative hypothesis is aided by identifying two types of errors (type 1 & type 2), and by specifying limits on the errors (e.g., how much type 1 error will be permitted).

Type I and Type II Errors 

A binary hypothesis test may result in two types of errors depending on test accepts or rejects the null hypothesis. The above two types of errors arise from the binary hypothesis test are

Type I error or false alarm: when H₀ is true, the researcher chooses alternate H_A.

Type II error or miss: when H_A is true, the researcher chooses H₀.

Figure-12: Type I and II Errors in hypothesis testing

Figure-13: Deciding H₀ and H₁

Test Statistic and Critical Region

A test statistic is often a standardized score such as the z-score or t-score of a probability distribution.

After setting up the hypothesis, the test statistic is computed using the sample observations. In case of large samples the test statistic approximates the normal distribution. However for small sample sizes, we may use other types of sampling distributions such as: t- distributions or F-distribution. The chi-square statistic is used for squared values such as the variance and squared errors.

The distribution of the test statistic is used to decide whether to reject or accept the null hypothesis.

Critical value of standardized score (z-score) or the Significance Level  divides the probability curve of the distribution of the test statistic into two regions – critical (or H₀ rejection) region and H₀ acceptance region. The area under probability distribution curve for the acceptance region is “1-α”. When the value of test statistic falls within acceptance region H₀ is accepted and when it falls with critical region H₀ is rejected. The threshold value of α is often set at 0.05, but can vary between 0.01 to 0.1.

Illustration of acceptance region and rejection region

In this situation, we were only interested in one side of the probability distribution, which is shown in the image below:

Figure-14: Region of acceptance and rejection of H₀

Figure-15: False Positive (False Alarm), False Negative (Missing) and Threshold value

An  ideal researcher minimizes the probabilities of errors  due to both Miss and False Alarm.

Inferential Statistic tests

Some commonly used inferential statistical tests are

1. t –test: used check if two independent sample distributions have the same mean (the assumptions are that they are samples from normal distribution).
2. F-test: used to test if two samples distributions have the same variance. The null hypothesis assumes that the mean of all sets normally distributed  populations,  have the same standard deviaton. The F-test was so named by George W. Snedecor in honor of Ronald A. Fisher and plays an important role in the analysis of variance ANOVA developed by Fisher. ANOVA is a generalization of hypothesis testing of the difference of two population means. When there are several populations multiple pair wise t-tests become cognitively difficult. The F-test statistic used in ANOVA is a measure of how different population mean values (variance between scatter) are, relative to variability with each group (variance within scatter).
3. Chi-Square test: can be used to test the independence of two attributes and difference of more than two proportions.
4. Regression analysis: determines the relationship between an independent variable (e.g., time) and a dependent variable (e.g., market demand of item).

Nonparametric Inferential Statistics methods are used when the data does not meet the requirements necessary to use parametric statistics, such as when data is not normally distributed. Common nonparametric methods include:

Mann-Whitney U Test: Non-parametric equivalent to the independent samples t-test.

Wilcoxon Signed-Rank Test: Non-parametric equivalent to the paired samples t-test.

Friedman test : Used for determining whether there are significant differences in the central tendency of more than two dependent groups. It is an alternative to the one-way ANOVA with repeated measures. The test was developed by the American economist Milton Friedman.

The Friedman test is commonly used in two situations:

1.     Measuring the mean scores of subjects during three or more time-points. For example, you might want to measure the resting heart rate of subjects one month before they start a training program, one month after starting the program, and two months after using the program.

2.     Measuring the mean scores of subjects under three different conditions. For example, you might have subjects watch three different movies and rate each one based on how much they enjoyed it.

These tests help to determine the likelihood that the results of your analysis occurred by chance. The analysis can provide a probability, called a p-value, which represents the likelihood that the results occurred by chance. If this probability is below a certain level (commonly 0.05), you may reject the null hypothesis (the statement that there is no effect or relationship) in favor of the alternative hypothesis (the statement that there is an effect or relationship).

 

References:

1. Fundamentals of Mathematical Statistics, SC Gupta and V.K. Kapoor
2. Operations Research an Introduction, Hamdy A. Taha
3. TB 1 EMC DataScience_BigDataAnalytics
4. https://www.toppr.com/guides/business-economics-cs/descriptive-statistics/law-of-statistics-and-distrust-of-statistics/

Figure Credits:

Figure-1: A sample of uses of statistics

Figure-2: Examples of nominal data, intellispot.com

Figure-3: Ordinal Data, questionpro.com

Figure-4: Interval Scaled Data,  questionpro.com

Figure-5: Ratio Scaled Data, questionpro.com

Figure-6:  NOIR attributes questionpro.com

Figure-7: Introduction to Statistics, Lat Trobe University Library.latrobe.libguides.com

Figure-8: Descriptive Statistics, Justin Zelster, zstatistics.com

Figure-9: Inferential Statistics, statisticaldataanalysis.net

Figure-10:  Comparing Distributions: Z Test, homework.uoregon.edu

Figure-11: What is inferential statistics, civilserviceindia.com

Figure-12: Errors in hypothesis, Six_Sigma_DMAIC_Process_Analyze, sixsigma-institute.org

Figure-13: H0 and H1 hypothesis testing, Inferential Statistics, mathspadilla.com

Figure-14: H0 accept or reject, homework.uoregon.edu

Figure-15: Making sense of Autistic Spectrum Disorders, Dr. James Coplan, drcoplan.com