Descriptive statistics
While raw data is a valuable resource, it is not often directly
usable due to several reasons. It may lack cohesion and can be cluttered making
it challenging to work with or understand. It may be human, machine, or
instrumental errors, depending on the collection method. It may be poorly
structured and hard to visualize. Often it may contain too much of data, which
cannot be sensibly analyzed.
Descriptive statistics refers to the analysis of descriptive statistic or
summary statistic. It helps to handle problems
associated with raw data in several ways: it can simplify data to make it represent
and understand, it can summarize and organize characteristics of a data set,
which helps in presenting the data in a more meaningful manner. Descriptive
statistics identifies central tendencies, variability, frequency distribution.
Descriptive summary statistics quantitatively describe or summarize features from a
collection of information so that the details and patterns in
data can be easily visualized.
To visualize summarization, we
can construct box plots and histograms to visually
describe the data. Any kind of charts, tables, and graphs, including frequency tables, stem and leaf plots, and pie graphs, would all qualify as
descriptive statistics. Descriptive statistics is not based on probability
theory and differs from inferential statistics which performs sampling and is
dependent on probability theory to derive conclusions.
Types of measures used in Descriptive statistics
Measures
of central tendency describe the central position of a data
distribution. The centre positions can be summarized using a number of
statistics, including the mode, median,
and mean. They could be called the three musketeers. The other measures are
geometric mean and harmonic mean. Measures of central
tendency alone are not sufficient to describe the data.
Figure-1: The 3 Musketeers – Measures of
central tendency
Measures of spread (variability) which summarizes how much the data values are
spread out from the centre. Describe spread, a number of statistics are
available, including the range, percentile,
quartiles, interquartile range, quantile, absolute deviation, standard
deviation, and variance.
Figure-2: Measures of Spread
o
Measure of shape
Measures of Shape are used to understand the pattern of how data is distributed. The pattern of distribution can be categorized into symmetrical distribution (e.g., Normal, Rectangular, U-shaped distribution etc) and asymmetrical distribution (skewed distribution). Skewness in a measure of asymmetry. Kurtosis is yet another shape descriptor that describes data in terms of its height or flatness.
Figure-3: Shapes can be measured
o
Measures of relationship
When there are multiple data features, we also need to
measure the relationship between them. There are several statistical measures
that can be used to capture how the feature are related to each other. The two
most widely used measures of how two variables move together (or do not) are Covariance
and Correlation.
Covariance between two data series (x1, x2,
…...) and (y1,
y2, …...), provides a
measure of the degree to which they move together. A positive sign indicates
that they move together and a negative sign that they move in opposite
directions. Correlation is the standardized measure of the relationship
between two variables. It can be computed from the covariance.
Correlation can never be greater than one or less than negative
one.
Figure-4: Relations can be measured
A
simple regression is an extension of the
correlation/covariance concept. It attempts to explain one variable, the
dependent variable, using the other variable, the independent variable.
Use
of descriptive statistics in analysis
Descriptive
summaries may be either quantitative i.e., summary statistics, or visuals such as simple-to-understand graphs etc. These
summaries may either form the basis of the initial description of the data as
part of a more extensive statistical analysis, or they may be sufficient in
themselves for a particular investigation.
For
example, in a basketball game the shooting percentage is a descriptive statistic that summarizes the performance of a
player or a team. This number is the number of shots successful divided by the
number of shots attempted. For example, a player who shoots 33% is making
approximately one shot in every three attempts. The percentage summarizes multiple discrete events. Consider also the grade point average. This single number describes the general
performance of a student across the range of topics learned during a course.
Univariate
analysis
This is perhaps the simplest form of
statistical analysis.
Like other forms of statistics, it can be inferential or descriptive. The key
fact is that only one variable (attribute/feature) is involved.
Univariate analysis involves
describing the distribution of
a single variable, including its central tendency (the mean, median and mode), dispersion (the range, interquartile range, variance and standard deviation etc) and the shape of the distribution may be described via indices
such as skewness and kurtosis.
Characteristics of a single variable's distribution may also
be depicted in graphical or tabular format, including histograms and stem-and-leaf display etc. The Frequency
polygon in figure give an idea about the shape of the data and the trends that the univariate
“Age” data set follows.
Figure-5: Univariate analysis (Frequency polygon)
Bivariate
analysis
Bivariate analysis is the simultaneous analysis of two
variables. It explores the concept of relationship
between two variables, whether there exist an association and the strength of
this association, or whether there are differences between two variables and
the significance of these differences.
When a sample consists of more than one variable,
descriptive statistics may be used to describe the relationship between pairs
of variables. In this case, descriptive statistics include:
- Cross-tabulations and contingency
tables.
- Graphical representation via scatter plots.
- Quantitative measures of dependence.
- Descriptions of conditional distributions
The
main reason for differentiating univariate and bivariate analysis is that
bivariate analysis is not only simple descriptive analysis, but also it describes the relationship
between two different variables.
Quantitative measures of dependence include correlation
(such as Pearson's r when
both variables are continuous, or Spearman's
rho if one or both are not continuous) and covariance. Slope in
regression analysis, also reflects the relationship between variables.
Figure-6: Bivariate analysis between
y1, y2
Multivariate analysis is
essentially the statistical process of simultaneously analyzing multiple independent (or predictor) variables
with multiple dependent (outcome or criterion) variables. Multivariate analysis (MVA)
is based on the statistical principle of multivariate statistics,
which involves observation and analysis of
more than one statistical variable at a time.
Figure-7:
Multivariate analysis
Role of moments in Statistics
Role
of moment in Statistics
Moments are
expected values of random numbers. In statistics, moments are quantitative
measures that describe the specific characteristics of a probability
distribution. They are used to determine the central tendency, variability and shape
of a dataset. Moments help to describe the distribution and are required in
statistical estimation and testing of hypotheses.
The jth moment (raw) of random variable xi which occurs with probability pi might be defined as the expected or mean value of x to the jth power. The jth central moment about x0, in turn, may be defined as the expectation value
of jth
power of the quantity x minus x0, i.e.,
First Moment (Mean): The first
moment is the mean or average of the data. The mean value of x is the first moment (j = 1) of
its distribution with x0 = 0. It measures the location of
the central point. It is defined as the sum of all the values the variable can
take times the probability of that value occurring.
Second Moment (Variance): The
second moment (j = 2) is the
variance. It measures the spread of values in the distribution or how far from
the normal.
Third Moment (Skewness): The
third moment (j = 3) is
skewness. It measures the asymmetry of the distribution. A positive skew
indicates that the tail on the right side is longer or fatter than the left
side. In contrast, a negative skew indicates that the tail on the left side is
longer or fatter than the right side.
Fourth Moment (Kurtosis): The
fourth moment (j = 4) is
kurtosis. It measures the “tailedness” of the distribution. High kurtosis means
that the data have heavy tails or outliers. Low kurtosis means that the data
are light tails or lack of outliers.
.
Measures of Central Tendency (Location)
Measures of central
tendency use a single value to describe the center of a data set. The mean,
median, and mode are all the three measures of the central tendency of the
population.
The mean, or average, is calculated by finding the sum of data values and
dividing it by the total number of data.
The median is the middle value in a set of data. It is calculated by first
listing the data in numerical order then locating the value in the middle of
the list.
The mode is the number that appears most frequently in the set of data or the
value with highest probability of occurrence. If no data appearing most
frequently there is no mode. If there are two data values occurring most
frequently then the data is bimodal, with three modes it is trimodal. For four
or modes it is multimodal.
Consider the
distribution of anxiety ratings of your classmates are 8, 4, 9, 3, 5, 8, 6, 6,
7, 8, and 10.
Mean: (8+ 4 + 9 + 3 + 5 + 8 + 6 + 6 + 7
+ 8 + 10) / 11 = 74 / 11 = 6.73.
Median : In a data set of 11 values, the
median is the number in the sixth place. This is computed by arranging the
values in their order i.e., 3, 4, 5, 6, 6, 7, 8, 8, 8, 9, 10. The median is 7.
Mode: The number 8 appears more than any
other number. The mode is 8.
The mean and median
can only be used with numerical data. The mean is not applicable for nominal
and categorically ordered data. The median is applicable for ordinal, interval
and ratio scaled data.
Figure-8:
Mean and Median on Box and Whisker plot
The mode can be used
with both numerical and nominal data in the form of
names or labels. Assume we go to fruit shop. The quantity distribution of
fruits in the shop is Mango -30, Apple -50, Pomegranate -20, Oranges -75. What
is the mode of the fruit distribution?
The mean is the most preferred
measure of central tendency (averages) since it considers all of the numbers in
a data set; however, it is extremely sensitive to outliers, or extreme
values that are much higher or lower than the rest of the values in a data set.
The median
is preferred in cases where there are outliers, since the median only
considers the middle values.
Other averages
The geometric mean is a type of mean or average, which indicates the central
tendency or typical value of a set of numbers by using the product of their
values (as opposed to the arithmetic
mean which uses their sum). The
geometric mean is defined as the nth
root of the product of n
numbers.
Figure-9: Geometric mean of p and q
The harmonic mean also called subcontrary
mean, is the reciprocal of the arithmetic mean of the reciprocal of data
values. If x1, x2, x3 are the data values, then harmonic mean is 3 x 1/(1/ x1,
+1/ x2, + 1/ x3). If any of these values
equals zero, the harmonic mean is zero. The harmonic is useful to compute the
average speed of a moving vehicle. Assume a cyclist moving at a speed of 20 km
per hour to his place of work and returns at a speed of 10 km/hr. If x is one way distance, then average speed is computed as 2 x x/(x/20
+ x/10)
Figure-10: Harmonic Mean
Percentiles, Deciles, Quantile, Quartile
Percentile divides
the number of observations in hundred equal parts and is a ninety nine point
measure to indicate the value of observations in the dataset below the
specified percentage. Deciles divide the
number to ten equal parts. It is a nine point measure, e.g. D7 indicates 70% of
observations are below it. Quantile values take regular percentage intervals of
the number of observations. Important Quantiles are
1.
Percentile
for 100-quantiles.
2.
Permiles
or Milliles for 1000-quantiles.
Figure-11:
Percentile and Quantile
Quartile is the value
of quantile at 25%, 50% and 75%. Therefore quartiles are 3 point measures. The
first quartile Q1 is the
median of the lower half i.e., the value
below which 25% of observations occur. The second quartile is Q2 median is the 50th
percentile. The third quartile Q3
the median of upper half i.e., the below which 75% of observations occur. Percentiles, quantile, quartiles are measures
that specify a score below which specific percentage of a given distribution
falls. These values are not applicable
for nominal data. They are not necessarily members of the data set
Figure-12:
Quartile
Assume a data set
{35, 22, 45, 53, 68, 73, 82, 19}. Arranging the numbers in their order we
get {19, 22, 35, 45, 53, 68, 73,
82}. Number of values below 25% level 2.
Hence Q1 = (22+35)/2 =
28.5. Similarly Q2 = (53+68)/2 = 60.5.
Measures of Dispersion
Measures of
dispersion are used to find how the data is spread out from a central value. The
most common measures of dispersion range, interquartile range, standard deviation
and variance.
Range
The simplest measure
of dispersion is the range. This tells us how spread out the data is. In order to
calculate the range, the smallest number is subtracted from the largest number.
Just like the mean, the range is very sensitive to outliers.
Interquartile
range
This is the range of
values between the first and third quartile or the range of the middle half and
less influenced by outliers.
Mean
Deviation
The
mean deviation (also called the mean absolute deviation) is the mean of the absolute deviations of a set of data about the
data's mean.
Mean deviation is an important descriptive statistic that is
not frequently encountered in mathematical statistics. This is essentially
because while mean deviation has a natural intuitive definition as the "mean
deviation from the mean," the introduction of the absolute value makes
analytical calculations using this statistic much more complicated than
the standard deviation.
As a
result, least squares fitting and other standard statistical
techniques rely on minimizing the sum of square residuals instead of the sum of
absolute residuals.
Standard Deviation (Root mean square deviation)
The standard deviation σ of
a probability distribution is defined as the square of the variance. The square root of the sample variance of a set of N values is the sample standard
deviation. The
square root of bias-corrected variance obtained by dividing by N-1 instead of N is also known as the standard deviation.
N-1 is the number of degrees of freedom
Assume we have a large dataset. The sum
of deviations of each sample value from the mean value will be zero. Therefore
if all values except for one are known, then the unknown value can be computed.
z-score
The z-score represents the value of
random variable data xn in
terms of the number of standard deviations above or below the mean of the set
of data
Variance
(Mean Square deviation)
Variance is the square of standard
deviance. It is calculated by summing the squared deviations for individual
data values from the mean and dividing it by the total number N of data values. This is called biased
variance. The bias corrected variance is computed b dividing N-1, which is the number of degrees of
freedom.
Measure of Shape – Skewness
A fundamental task in many
statistical analyses is to characterize the location (mean) and variability of
a data set. A further characterization of the data includes skewness and
kurtosis. Skewness measures the shape of a distribution.
Skewness is a measure of asymmetry,
the lack of symmetry or deviation from normal distribution. A distribution, or
data set, is symmetric if it looks the same to the left and right of the center
point.
Definition of skewness
Skewness is asymmetry in a
statistical distribution, in which the curve appears distorted or skewed either
to the left or to the right. Skewness
can be quantified to define the extent to which a
distribution differs from a normal distribution. The value for skewness is referred
to as the Fisher-Pearson coefficient of skewness.
The skewness for a normal
distribution is zero, and any symmetric data should have skewness near zero.
Negative values for the skewness indicate data that are skewed left and
positive values for the skewness indicate data that are skewed right. By skewed
left, we mean that the left tail is long relative to the right tail. Similarly skewed
right means the right tail is longer relative to the left tail. If the data are
multi-modal, then this may affect the sign of the skewness.

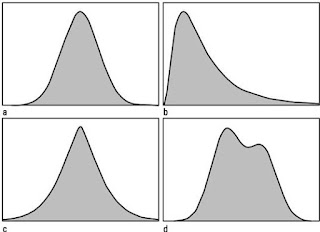
Figure-13:
Skewness
In the
above figure first one is moderately skewed left: the left tail is longer and
most of the distribution is at the right. By contrast, the second distribution
is moderately skewed right: its right tail is longer and most of the
distribution is at the left.
Skewness
coefficient for any set of real data almost never comes out to exactly zero
because of random sampling fluctuations. A very rough rule of
thumb for large samples is that if gamma is greater than
4/sqrt(N)
then
the data is probably skewed.
Skewness for a
normal distribution is zero, and any symmetric data should have a skewness near
zero. Negative values for the skewness indicate data that are skewed left and
positive values for the skewness indicate data that are skewed right. By skewed
left, we mean that the left tail is long relative to the right tail. Similarly,
skewed right means that the right tail is long relative to the left tail. If
the data are multi-modal, then this may affect the sign of the skewness.
Figure-14:
Positive and negative Skewness
Measure of Tailedness –
Kurtosis
Kurtosis is a measure of whether
the data are peaked or flat relative to a normal distribution. That is, data
sets with high kurtosis tend to have a distinct peak near the mean, decline
rather rapidly, and have heavy tails. Data sets with low kurtosis tend to have
a flat top near the mean rather than a sharp peak. A uniform distribution would
be the extreme case of flat top.
The histogram is an effective graphical technique for
showing both the skewness and kurtosis of data set.
Definition of Kurtosis
Kurtosis is a measure of flatness or peakedness of the distribution. It is a
measure of whether the data has heavy tails or light tails compared to the
normal distribution. Datasets with high kurtosis tend to have heavy tails to
include outliers, the uniform distribution is an extreme case of high kurtosis.
Datasets with low kurtosis tend to have light tails and indicates lack of
outliers. Karl Pearson calls kurtosis the “convexity of a curve”.
Alternate Definition of Kurtosis (Excess 3 Kurtosis)
The kurtosis
for a standard normal distribution is three. For this reason, some sources use
the following definition of kurtosis (often referred to as "excess
kurtosis"):
The kurtosis of standard normal distribution is 3, The excess 3 kurtosis is
used so that the standard normal distribution equals zero. In addition, with
this second definition positive kurtosis indicates a "peaked"
distribution and negative kurtosis indicates a "flat" distribution.
Which definition of
kurtosis is used is a matter of convention. The code writer needs to be aware of which
convention is being followed. Many sources use the term kurtosis when they are
actually computing "excess kurtosis", so it may not always be clear.
The three distributions shown below happen to have the same
mean and the same standard deviation, and all three have perfect left-right
symmetry (that is, they are unskewed). But their shapes are still
very different. Kurtosis is a way of quantifying these
differences in shape.
Figure-15:
Kurtosis
Measures of Relationship (correlation or association)
Correlation coefficients are measures of the degree of relationship between two or more
variables. It is the manner in which the variables tend to vary together. For
example, if one variable tends to increase at the same time that another
variable increases, we would say there is a positive relationship between the
two variables. If one variable tends to decrease as another variable increases,
we would say that there is a negative relationship between the two variables.
It is also possible that the variables might be unrelated to one another, so
that there is no predictable change in one variable based on knowing about
changes in the other variable.
A relationship between two variables
does not necessarily mean that one variable causes the other. When there is a
relationship, there are three possible causal interpretations. If we label the
variables X and Y, X could cause Y, Y
could cause X, or a third variable Z could cause both X and Y. It is therefore
wrong to assume that the presence of a correlation implies a causal
relationship between two variables.
Scatter Plots
To visualize a
relationship between two variables a scatter plot
is constructed. A scatter plot represents each set of paired scores (values) on a two
dimensional graph, in which the dimensions are defined by the variables.
Figure-16:
Correlation in bivariate data
Coefficient of
correlation vs Predictive power coefficient
The coefficient of correlation is a widely used measure of
the “goodness of fit”. Higher this value, better this measure. It is therefore
used for predict purposes or to predict the changes of one variable e.g.,
dependent variable or extrapolating the fitted function beyond the range of
observations. However this assumption is not always valid a better method will
be to use the predictive power score.
Figure-17: Negative,
Zero and Positive correlation
Covariance of a
bivariate population
Covariance between two features x and y is a measure of the tendencies of both features to vary along the
same direction.
The covariance is related to the Pearson correlation coefficient.
Figure-18: Positive and
Negative covariance
Pearson Product-Moment
Correlation
The Pearson product-moment
correlation was devised by Karl Pearson in 1895, and it is still the most widely
used correlation coefficient.
The Pearson product-moment correlation is an index of the
degree of linear relationship between two variables that are both measured on
at least an ordinal scale of measurement.
The index is structured so that a correlation of 0.00 means
that there is no linear relationship, a correlation of +1.00 means that there
is a perfect positive relationship, and a correlation of -1.00 means that there
is a perfect negative relationship.
As you move from
zero to either end of this scale, the strength of the relationship increases.Correlation index can be visualized as the strength of a
linear relationship or how tightly the
data points in a scatter plot cluster around a straight line. In a perfect
relationship, either negative or positive, the points all fall on a single
straight line.
The symbol for the Pearson correlation is a lowercase “r”, which is often subscripted with the
two variables. For example, rxy would stand for the correlation
between the variables X and Y.
The Pearson product-moment correlation was originally
defined in terms of Z-scores. In fact, you can compute the
product-moment correlation as the average cross-product Z, as show in the first equation below.
Spearman Rank-Order
Correlation
The Spearman rank-order
correlation provides an index of the degree of linear relationship between two
variables, that are both measured on at least an ordinal scale of measurement.
If one of the variables is on an ordinal scale and the other is on an interval
or ratio scale, it is always possible to convert the interval or ratio scale to
an ordinal scale.
If,
for example, one variable is the rank of a college basketball team and another
variable is the rank of a college football team, one could test for a
relationship between the poll rankings of the two types of teams: do colleges
with a higher-ranked basketball team tend to have a higher-ranked football team?
A
rank correlation coefficient can
measure that relationship, and the measure of significance of the rank
correlation coefficient can show whether the measured relationship is small
enough to likely be a coincidence.
If
there is only one variable, the rank of a college football team, but it is
subject to two different poll rankings (say, one by coaches and one by
sportswriters), then the similarity of the two different polls' rankings can also
be measured with a rank correlation coefficient.
The Spearman correlation has the same range as the Pearson
correlation, and the numbers mean the same thing. A zero correlation means that
there is no relationship, whereas correlations of +1.00 and -1.00 mean that
there are perfect positive and negative relationships, respectively.
References:
1.
Fundamentals of Mathematical
Statistics, SC Gupta and V.K. Kapoor
2.
Operations Research an
Introduction, Hamdy A. Taha
3.
TB 1 EMC DataScience_BigDataAnalytics
4.
https://www.toppr.com/guides/business-economics-cs/descriptive-statistics/law-of-statistics-and-distrust-of-statistics/
5.
https://www.itl.nist.gov/div898/handbook/eda/section3/eda35b.htm
Figure Credits:
Figure-1: Three
Musketeers , newsphonereview.xyz
Figure-2:
Measures of Spread news.mit.edu
Figure-3:
Shapes can be measured, The symmetry and shape of data, dummies.com
Figure-4:
Relations can be measured, What does it mean if correlation coefficient
positive negative or zero, investopedia.com
Figure-5: Univariate analysis (Frequency polygon),
Statistical concepts – Graphs, ablongman.com
Figure-6: Bivariate analysis between
y1, y2, Univariate and Bivariate analysis, slideserve.com
Figure-7:
Multivariate analysis, creative-proteomics.com
Figure-8:
Mean and Median on Box and Whisker plot, Diagram of Box plots components,
researchgate.net
Figure-9: Geometric mean of p and q, en.wikipedia.org
Figure-10: Harmonic Mean, educba.com
Figure-11:
Percentile and Quantile, Essential basic
statistics machine learning data science,
snippetnuggets.com
Figure-12:
Quartile, slideshare.net
Figure-13:
Skewness, The symmetry and shape of data distributions often seen in
biostatistics
dummies.com
Figure-14:
Wikipedia.org
Figure-15:
Kurtosis, Leptokurtic or platykurtic degree
difference of curves with different kurtosis, researchgate.net
Figure-16:
Correlation in bivariate data, Spearmans rank order correlation statistical
guide statistics.laerd.com
Figure-17:
Negative, Zero and Positive correlation, statisticsguruonline.com
Figure-18: Positive
and Negative covariance, youtube.com



















I was trying to learn some stats from other online channels. Your blog perfectly captures all the elements of statistics you need for Data Science! Thank you!
ReplyDelete