Probability and Statistics for Artificial Intelligence and Machine Learning Part-2

Probability Mass Function for Discrete Valued Variables

A discrete variable is a variable which has countable number of specific values. The probability distribution of a discrete random variable “X” is a list of probabilities associated with each of its possible values. When a specific value observed for X it is denoted by “x_k”. The probability distribution of a discrete valued variable is called a probability mass function and is also known as discrete density function.

Consider when a random variable X can take values equal to x₁ = 4, x₂ = 5, x₃ = 6 or x₄ = 7  and so on.

Figure-1: Example of a PMF

Some examples of discrete probability distributions are Bernoulli, Binomial, Negative Binomial, Poisson, Geometric, Hypergeometric, Multinomial, etc.

Probability Distribution Functions of continuous valued variables.

The probability distribution of a continuous random variable is known as probability density function or density of continuous random variables. When the random variable is continuous valued the probability of observing any single or specific value equals 0, since the number of possible values for that random variable is infinite.

A random variable X may take all values over an interval of real numbers. When a specific value observed it is denoted by “x”. This means X = x. The curve, which represents a function p(x), must satisfy the following: 

1. With no negative values, p(x) > 0 for all x.
2. The total area under the probability curve over the entire interval equals 1.

A curve meeting these requirements is known as a density curve.  Consider that a ≤ x ≤ b, and that the set of values observations (outcomes) a to b, is denoted by A. Then  f(A) is defined to be the area under the curve A.

Some examples of continuous probability distributions are normal distribution, exponential distribution, beta distribution, etc.

Figure-2

Cumulative mass functions and cumulative density functions

Cumulative density function is another method of describing the probability of continuous valued random variables (Cumulative mass functions for discrete rvs. It is the probability of that the random variable X takes less than or equal to a specific value. For continuous random variables it computed by integrating the area under curve until x. For a discrete random variable, the cumulative distribution function is found by summing up the probabilities until x_k.

 Figure-3: pmf and its cmf

 Figure-4: pdf and its cdf

Important distributions

Discrete Distributions

The binomial and Bernoulli distributions

The binomial distribution is a discrete probability distribution which has only two outcomes. It models the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p.  As examples consider that a new drug is introduced to cure a disease, it either cures the disease (it’s successful) or it doesn’t cure the disease (it’s a failure). Or if you purchase a lottery ticket, you’re either going to win money, or you aren’t. Anything you can think of that can only be a success or a failure can be represented by a binomial distribution.

The simplest example of visualizing a binomial experiment is the toss of a two-sided coin. Consider you toss the coin “n” times. If the coin is perfectly balanced, then the probability “p” of observing any side is the same i.e., probability of observing heads (success) or tails (failure) equals 0.5. If the coin is not balanced the p ≠ 0.5.

A binomial experiment has to satisfy the following four conditions

1. The experiment consists of n identical trials.
2. Each trial results in one of the two outcomes, called success and failure.
3. The probability of success, denoted p, remains the same from trial to trial.
4. The n trials are independent. That is, the outcome of any trial does not affect the outcome of the others.

Consider you conduct an experiment with probability of “heads” equals 0.25. You do the trial n = 20 times and plot the histogram for probabilities of observing heads 0 – times to 20 – times. 

 

Figure-4: Histogram of binomial distribution

Figure-5: Binomial distribution

The above plot shows the distribution of m = 15 successes out of n trials with p = 1/2.

Some examples in daily life for binomial distribution

1. A drug company tests the performance of a new drug. 
2. A restaurant sells vegetarian and non-vegetarian sandwiches. 80% of sandwiches sold are non-veg, you may find the probability 2 out of 5 customers will choose non-veg.
3. An automobile company finds that 70% customers of a particular model is men. What is probability that out of 10 car owners randomly picked 5 are men.

Bernoulli Distribution

The Bernoulli distribution has only two outcomes either 1 or 0. The number of trials n = 1. If the observation of trial equals 1, then it is considered success otherwise the outcome is a failure.

 Figure-6: Histogram of Bernoulli Distribution

When a lottery ticket is purchased what is the probability of winning, how is  it modeled, Bernoulli or binomial?

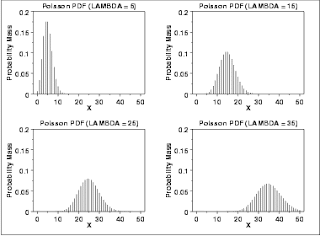
Poisson Distribution

Named after the French mathematician Siméon Denis Poisson the Poisson random variable is typically used to model the number of occurrences of an event within a fixed space/time interval. Thus, the Poisson distribution is a discrete probability distribution used to compute the probability of events occurring in a given unit of time/region (distance, area or volume),  if these events occur with a known constant mean rate and independently of the time or space since the last event.

It can be used to estimate how likely an event will happen k number of times if the average rate is λ > 0. This is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event

Figure-7: Poisson distribution for various values of λ.

Some real life applications of Poisson distribution

Insurance

Insurance companies often conduct risk analysis on traffic accidents using average crash accidents within a fixed time window, and use it to inform the pricing of car insurance.

Number of customers at a service counter
Customers arrive at a hypermarket cash counter at random. With average number of customers reaching within a fixed interval of time (e.g. ½ an hour) being denoted by λ, Poisson distribution can be used to compute the probability of x = k customers arriving within the same interval of time. 

Web traffic
Page requests per second to a website. Modeling it with a Poisson distribution could be very helpful for detecting spam attacks (anomaly detection) or estimating peak load given average load.

Authorship dispute
An investigating agency was appointed to determine the authorship of a federal document claimed to be written by two authors - Hamilton or Madison. They  looked at rates of usage of specific words in Hamilton's and Madison's other papers, then found consistent patterns in the rates at which each author used these words. They found, for example, that Madison (in his other writings) tended to use "upon" around once every six thousand words, while Hamilton used it around three times every thousand words.
They then compiled a list of words useful for distinguishing Hamilton and Madison's writings, then used this (together with statistical tests using the Poisson and Binomial distributions) to conclude that Madison was almost certainly (with odds a million to one) the author of all the disputed Federalist Papers.

Continuous distributions

Continuous uniform distribution

The continuous uniform distribution or rectangular distribution is a symmetric probability distribution that has constant probability over a certain interval. The distribution describes the outcome of an experiment that results in arbitrary values which lies between certain bounds.

Figure-8: Uniform distribution

Real life examples

1.      The number that comes up from the roll of a fair die.

2.      The first number picked for the lottery.

3.      A metro trains on a certain line run every half hour between mid night and six in the morning. What is the probability distribution to model that a person entering the station at a random time during this period will have to wait at least twenty minutes?

Gaussian  (Normal) Distribution 

Named after the German mathematician Carl Friedrich Gauss, the Gaussian (Normal) distribution ubiquitous in Machine learning is a probability density function. For a scalar random variable x it is defined as

A normal distribution has a bell-shaped density curve described by its mean μ and standard deviation σ. Hence it is a two parameter probability distribution. The density curve is symmetrical, centered about its mean, with its spread determined by its standard deviation showing that data near the mean are more frequent in occurrence than data far from the mean. 

Figure-9: Gaussian distribution

Almost 68% of the data falls within a distance of one standard deviation from the mean on either side and 95% within two standard deviations. When mean = 0 and standard deviation = 1 it is called a standard normal distribution.

Real life examples

Height of population. 

Figure-10:

                                                       

Rolling a dice curve (multinomial takes the form of  Gaussian)

Figure-11:

Tossing a coin Binomial and Gaussian

Figure-12

IQ Score

Figure-13

Stock Market

Figure-14

Income distribution of society

Figure-15

Weight at birth

Figure-16

Performance Appraisals

Figure-17

The Central Limit Theorem

One of the most profound and fundamental theorems in statistics and may be in all mathematics. It is one of the most remarkable results of the theory of probability. In its simplest form, the theorem states that the sum of a large number of independent observations from the same distribution, under certain general conditions, has an approximate normal distribution. . In other words ,the sampling distribution of the sample means approaches a normal distribution as the sample size gets large, no matter what the distribution of the population distribution.

Figure-18

Gamma distribution

Gamma distribution is also belongs to two parameter family of continuous distributions. However it is defined only for positive real valued random variables that is x ≥ 0. It arises naturally in processes for which the waiting times between events are relevant. It can be thought of as a waiting time between Poisson distributed events, where θ is the mean time between events. Gamma distribution is rarely used in its raw form. Popular special cases are Exponential, Erlang and Chi-squared distribution.

The gamma family of distributions is family of distributions on [0,∞) which can be derived from the gamma functions. It is defined in terms of two parameters – the shape k > 0 and the rate of change (or mean time between two events) θ > 0.

Figure-19: Gamma distribution with various values of k and θ.

Plot of gamma distribution for various values of shape and scale parameters

It is defined in terms of two parameters – the shape k > 0 (in python code a = k) and the rate of change (or mean time between two events) θ > 0. The shape parameter will affect the shape of a probability distribution rather than simply shifting it (as a location parameter does). The reciprocal of θ is called the scale parameter which is used for stretching/shrinking it. For k > 1, the distribution tends to take a bell shaped form.

Real world examples

§  The amount of rainfall accumulated in a reservoir

§  The size of loan defaults

§  The aggregate insurance claims

§  The flow of items through manufacturing and distribution processes

§  The load on web servers

§  The many and varied forms of telecom exchanges to model the multi-path fading of signal power.

§  In neuroscience, the gamma distribution is often used to describe the distribution of neuron inter-spike intervals.

Exponential distribution  special case of the Gamma distribution where k = 1

The exponential distribution is used to model the time intervals between events in a Poisson process.

Figure-20: Exponential distribution

Beta distribution

The beta family of distributions is family of distributions on [0,1] with parameters . In order to ensure that the distribution is integrable it is required that the beta distribution is to model events which are constrained to take place within an interval defined by a minimum and maximum value.  This is a continuous distribution that has a support over the interval [0,1]. 

It is one of the few distributions that gives the probability equals 1 over a finite interval  [0,1]. Hence it is often used to model proportions. The values of proportions naturally lies between [0, 1].

Figure-21

Beta distribution as a function of x =  μ for various values a and b.

In order to ensure that the distrib ution is integrable and B(a,b) exists, both a, b must be > 0.

If  a = b = 1  we get uniform distribution.

If a, b < 1 then we get a distribution that peaks at 0 and 1.

If a, b > 1, then we have uni-modal distribution. (consider a=2,b=3).

The Multivariate Gaussian

This is the most widely used joint probability density distribution for continuous variables. The multivariate generalization of a Gaussian pdf in the D - dimensional space 

Figure-22: Multivariate Gaussian 

Figure Credits:

Figure-1: Basics of statistics, transtutors.com 

Figure-2: Introduction to Statistics – Thomas Halswanter 

Figure-3: Topics in mathematics Probability Mass Functions,  sciencedirect.com

Figure-4: Combined cumulative distribution graphs,  common.wikimedia.org

Figure-5: Binomial distribution, real-statistics.com

Figure-6: Binomial Distribution,  mathworld.wolfram.com

Figure-7: Engineering Statistics Handbook, itl.nist.gov, 

Figure-8: Wikipedia.org

Figure-9: Computer Vision for dummies Vincent Spruyt,

Figure-10: What is a normal distributions, thougthco.com

Figure-11: math.stackexchange.com

Figure-12: Binomial Probability Normal Curve, athbitsnotebook.com

Figure-13: futuretimeline.net

Figure-14: Predicting Stock Market Returns - Lose The Normal And Switch To Laplace Vance Harwood

Figure-15: Forbes.com

Figure-16: Introduction to Statistics for Clinical Trials: Standard error and confidence intervals, user.york.ac.uk

Figure-17: studiousguys.com

Figure-18: Central limit theorem, medium.com

Figure-19: Plot of gamma distribution for various values of shape and scale parameters,Wikipedia

Figure-20: Wikipedia.org

Figure-21:Wikipedia.org

Figure-22: Beta distribution as a function of x =  μ for various values a and b., boost.org