Gradient Descent rule and Widrow Hoff rule for Deep Learning

(PLEASE READ THE PREVIOUS POST ON ARTIFICIAL NEURAL NETWORKS AND ITS LEARNING ALGORITHMS)

Adapting the weight of a linear neuron (Adaptive Filtering Problem)

A Perceptron network single neuron unit with threshold logic unit activation has a discrete two valued outputs,  each one to represent a distinct class. The main objective of Perceptron network training is to find a feasible w* that separates the two classes. The learning algorithm progressively reduces the distance between the updated weight vector to the set of feasible weight vector solutions. However a single neuron operating with a linear activation function can perform like an adaptive filter. 

Figure-1

Adaptive Filtering

The Least Mean Squared (LMS) also known as the Delta rule or the Widrow Hoff rule is the basis of implementing a linear adaptive filtering. The aim is to minimize the squared errors over all the training data samples and therefore is a convex optimization problem. The LMS algorithm ensures that the weight values are adjusted so that the actual output values from the network moves closer to the desired  targets or true values by minimising the output error. The delta rule for updating the weight values can be applied even to non-linear neurons and to solve non-convex problems.

Figure-2

Convex vs Non-convex

Modelling an unknown dynamic system

Consider a dynamical system, with a multidimensional input signal and single output function as shown in Figure-3. Assume that the mapping function between the input and output is not known.

A multiple input-single output model of the unknown linear dynamical system can be built around a single linear neuron.

Figure-3

LMS modeling an unknown dynamic system

The external input output behaviour of the unknown dynamic system is described by the data set

     τ: { s(n), d (n)}: n = 1,2, …, N} where s(n) = {s₁(n), s₂(n), ….. s_d (n)} is the set of inputs and d (n) is the corresponding set of known targets.

The input samples s(n) in the data set τ are identically distributed according to an unknown probability distribution. The input space that generates s(n) is I dimensional vector space.

An adaptive linear filter modeling system adjusts the synaptic weights under the influence of a control (gradient descent) algorithm. The operation of this adaptive filter can be divided into two continuous processes.

Consider the m^th iteration

 1) Filtering process: This involves the computation of two signals

     a) An output y(m) is produced in response to I +1 elements (bias included) of the augmented input           vector s(m), that is 

    b) An error signal e(m) is obtained by comparing the output  y(m) with corresponding desired                output  d(m), that is e(m) = d(m) – y(m)

2) Adaptive process: This involves the automatic adjustment of the synaptic weight vector w(m) in accordance with the error e(m)

The combination of these two processes working together constitutes a kind of feedback loop acting around the network. (Note: This is not a feedback signal in the usual sense since output is not fed back directly to the network input).

The neuronal model described above is referred to as an adaptive filter. Minimization of network error is an optimization problem.

The training sample response d_n may contain two types of noises 1) individual samples from the entire population of the system output distribution may deviate from true values due to random noise, these are systemic errors and 2) the selected samples may not be true representatives of the true output population, this type of error is called sampling error.

The method Gradient descent rule  for error function optimization

The gradient descent rule is the simplest derivative based optimization algorithm which is performed iteratively. The objective function to be optimized is the squared error function. At every iteration, the weight vector is updated by a small change vector Δw(m) in accordance with the gradient of the objective function and hence it is also called delta rule. Since this delta rule tries to minimize the squared errors this learning algorithm is called the Least Mean Square (LMS) algorithm  proposed by Bernard Widrow and Ted Hoff (1960).

Gradient descent rule is an example of unconstrained LMS algorithm. Gradients of objective function E(w(m)) w.r.t the “I +1” dimensional  w(m) makes another vector that contains all partial derivatives of the objective function with respect to individual components of w(m). The objective function E(w(m)) performs a mapping from the "I + 1" space R^I +1 (which  is (I +1)-dimensional weight vector space which includes the bias) to a one-dimensional space R that results in a scalar value.  

The well known weight/parameter update equation as per this rule is given as 

This is equivalent to

 

Figure-4

Gradient descent in 2D weight space

The above figure illustrates partial derivatives computed at an iteration step in a two-dimensional weight space. As the error function approaches to a minimum value its gradient w.r.t to w decreases, hence the magnitude of the weight update also decreases.

Feature processing

It is important to pre-process the features for faster convergence of gradient descent algorithms and good model performance. As an example assume there are two independent features s₁ with a range of values [0 – 3000] and the s₂ with [0-100]. The larger magnitude features exert greater influence on the total error and the weight adaption at every iteration step. Characteristics of features though with lesser which also hold information about data will tend to get ignored. There are various methods of feature processing. For details read earlier article on "Data preparation methods"

The linear neuron with squared error surface

For a linear neuron with squared error has a quadratic error surface function. The contours of this surface are the loci of constant error values will be elliptical. They are called equal error contours. Consider a two dimensional  weight space with w₁ and w₂ axes. The equal error contours are elliptical as shown in figure since the rate of change of error along each of this axis is different. If rate of change in both directions are equal (not a general case) the contours will be circular.

Figure-5

Error contours of a linear neuron vs. w (2D vector)

For a network with linear activation function with no bias, the error squared vs. the weight graph is a paraboloid that passes through the origin in “I - dimensional” space. 

Since the proportionality constant is negative due to gradient descent, the graph of such a function is convex downward (or concave upward) and has a minimum value. The vertex of this parabolic surface represents the point where the error is minimum. The weight vector corresponding to this point is then the ideal weight vector w*. The following figures illustrates the downward convexity of the parabolas with respect to individual weights  w₁ and w₂.  

Figure-6

Error function of a linear neuron vs. w₁ and w₂ axes of the ellipse

The error function of a linear neuron exists in a multidimensional vector space with the horizontal hyperplane defined by independent weight variables (a.k.a free parameters) in a multidimensional space and the vertical axis (height) correspond to the error function values.  For a linear neuron with squared error function, the error surface is a smooth quadratic bowl and will have global minimum. Vertical cross sections are parabola as shown in figure above and horizontal cross sections are ellipses.

Online and Offline learning methods

The learning method can be done in two fundamentally different ways 

1. Stochastic (Online) learning: - In this method the input output data pairs of [s(n), d(n)] are chosen one a time. At the n^th sampling instant, the current training data set represents the past (n - 1) and the present (n) values. Error is computed and weight values are updated at every signal presentation. Hence the online method can adapt to all the signal statistics or the input environment and can function like an online adaptive filter. 
2. Batch (Offline) learning: - A set of N sample pairs [s(n), d(n)] that originate at different points in input space is collected at a time. This is a snapshot of data vectors. The total error for this collection of data is computed to update the weight values. Hence it is called offline learning or adaptation.

Least Mean Square Algorithm

The  LMS algorithm was originally proposed by Bernard Widrow and M.E (Ted) Hoff in 1960 to train the parameters of adaptive linear neurons. Hence it is known as the Widrow Hoff learning rule or Delta learning rule or the Adaline rule, is one of the most commonly used learning rules. It is so called because it adjusts its weights so as to minimize the mean squared error.  This method is based on the steepest descent algorithm.

The algorithm is provided with the data set   τ : { s(n), d (n)}; n = 1,2,…,N} and is an example of supervised learning method. The samples in the data set are independent of each other and identically distributed (i.i.d). For a given input sample data vector, the output from the network is compared to the corresponding output from the unknown dynamic system. If the difference is zero, no learning takes place; otherwise, the weights are adjusted to reduce the mean square error.

One complete presentation of all N training pairs in the set during learning process is called an epoch.

The LMS algorithm is the simplest learning rule derived from the mean square error MSE criterion. It is an adaptive algorithm since it computes the weight change required based on the current value of the error. Therefore it can adapt to the environment even if it is not ergodic (stationary). The current value of error can depend on the current status of the environment.

Online learning – Stochastic Gradient descent (Pattern-by-Pattern learning) for multiple linear neurons (linear regression model)

The derivation of the above delta rule for a network with K output neurons is straight forward. The output error for K neurons can be computed as (we use “m” to denote the iteration step)

     

The change in weight of the synapse connected between the i^th input to the k^th output  unit is given below. (As an exercise the reader may try to modify this equation for a single neuron network).

 

The cap over “w” indicates that the computed value is an estimate.

Merits and Demerits

Updates the model for every data sample observed, hence stores the experience of all the input output samples in data set. Though computation of weight change in each step is faster compared to batch gradient the method takes long time to complete an epoch if data set is large. The training is said to have completed an epoch when the N samples in the data set is presented. For online method total number of iterations to complete an epoch equals N. Since the model learns signal characteristic of every data sample observed, the model fits even the noises in data. This reduces the accuracy on test data though it will be high on train data.  

Figure-7

Full batch (off line) (a.k.a steepest descent) learning for multiple neurons

Batch learning method computes the total output error for the entire training data set for the network  which is expressed as  

 

The derivative with respect to the i^th weight vector to the k^th output neuron can be computed using the chain rule

Merits and Demerits

For batch method gradient steps are smoother and requires only fewer updates since update is done after all samples are observed. The method filters out the noise in data and fits to the true characteristics of only the data ignoring the noise. Every training step requires large memory space and speed can be slow for large datasets. Chances of converging to local minima is higher.

Scope of above equations for deep learning

The weight update equations discussed can only be used for a network with only for single layer network with output units or the output layer neural network if multi-layered  feedforward neural network. To access and to update weights of the inner layers we need to use the back propagation algorithm.

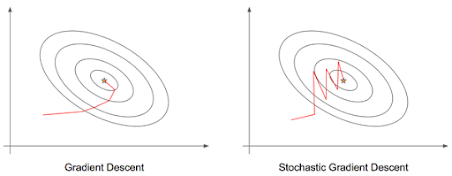
Error trajectory Online vs Offline methods

The initial location on the error surface will dependent on the initial set of weight values. The path of the error movement depends on the shape of the error surface, the value of the learning rate and also whether the method is on-line or off-line.

The gradients of the error surface with respect to the independent directions of the weight vector will differ for each direction and the resultant gradient will be oriented more in the direction of largest gradient. In Figure-6 above the directional derivative of the error surface is lesser along the w₁ axis compared to the w₂ axis. In multiple dimensions therefore the derivatives at each point will differ along the different directions. If however surface contours are purely circular the all partial derivatives will have the same value.    

For online method the algorithm computes synaptic weight adjustments and approximates the method of offline method batch gradient descent or true steepest descent. It does not compute the exact gradient (steepest) descent, but only produces an estimate of the weight vector. Therefore for on-line method the weight vector traces a random trajectory. As a result the direction of error movement may not point always towards the true minimum. The error trajectory during this method zigzags around the direction of steepest descent. Hence the on-line is also called a stochastic gradient algorithm (SGD). 

Figure-8

During batch learning the weights are updated after adding the errors due to all samples of the training data. Therefore the expected value of gradient over a set of iterations will equal the steepest gradient direction. The off-line method the weight vector trajectory follows a definite path unlike the online which follow a random path. Hence the gradient descent will move in a direction that contains the average information of all directions and follows the steepest descent path that is perpendicular to the error contours.

Mini Batch method: The disadvantage for both on-line and full batch training is that the convergence speed is very slow. A solution to speed up the training with gradient descent method is by updating weight values after summing the errors over smaller sets (mini batches) of training data samples. The weights are updated after summing the squared errors over each mini-batch. Hence this method is called mini-batch training. This method is more popular than the on-line method and full batch method.

Figure-9

Merits and Demerits

It has the combined benefits of both stochastic and batch gradient methods and minimizes the demerits. Weight updates are less frequent than stochastic method but more than batch method. But on large data sets since gradients are computed for smaller subsets of entire data it is faster than batch method. Chances of converging to local minima is lesser than compared to batch method and achieves more accuracy than stochastic method since noise in data is averaged out in small batches. However deciding the batch size is critical. Most common mini batch size is 32 data samples per batch.

Figure-10

Error surface for non-linear units

For multi-layer feedforward with non-linear activation units, the error surface is much more complicated and apart from the existence of a global minimum, it may have multiple local minima (McInerney and Dhawan 1989). The error surface may contain many several valleys and troughs.

The error function of linear regression problem is always convex in shape, hence it always has a global minimum unlike the non-linear regression problem where there can be many local minima. 

Figure-11

However as it can be seen from the above figure even for nonlinear multilayer networks the error surface is locally quadratic.

A good performance measure for regression networks is the standard deviation of errors which should be at least an order of magnitude lesser than the standard deviation of target values. The ratio of standard deviation of errors w.r.t standard deviation of target values is a good ranking index for regression networks.

Effect of Learning rate (η)

The best value of the learning rate depends on the shape of error surface. If η is small enough then the final weight vector w* can store the experience due to all the inputs used during training. Thus the weight values will memorize the knowledge of the entire input environment. However for small values of η, convergence will be slow. The mean error path will be a smooth and the transient response of the system is then over damped.

 

Figure-12

With large values of η convergence will be faster and final weight vector w* stores the knowledge of only current values and the recent past values of the input. Transient response may become oscillatory due to under damping. If   η exceeds a certain critical limit, then the algorithm will become unstable and behave like an oscillator.

This article introduced the gradient descent algorithm and how it is used to update the parameters of a single layer neural network that can model a mapping of the input to a continuous valued output as in case of regression problems. It is evident the weight update equations described above are valid only for the output layer synapses and cannot be directly applied for those of  the hidden layers. The next article on Back Propagation algorithm describes how to update the synaptic weights of any layer of multi-layered neural network. 

References:

1. Simon S. Haykin, “Adaptive Filter Theory” , 4^th Ed, Pearson Education.
2. Laurene V. Fausett, “Fundamentals of neural networks”, 1994,  Pearson Education.
3. Simon S. Haykin, “Neural Networks and Learning Machines”, 2^nd Ed, Pearson Education.
4. Bernad Widrow, Standford University, Rodney Winter, USAF, Neural Network for Adaptive Filtering and Adaptive Pattern Recognition
5. D. Joyce, Directional derivatives, steepest ascent, tangent planes, Math 131 Multivariate Calculus, Clark University
6. Petar Milin¹, Harish Tayyar Madabushi², Michael Croucher³, Dagmar Divjak⁴, “Keeping it simple: Implementation and performance of the proto-principle of adaptation and learning in the language sciences”, ^1,2,3 University of Birmingham, UK, ⁴ Numerical Algorithms Group, UK,

Image Credits

Figure-2: www.oreilly.com

Figure-8: www.quora.com

Figure-9:  seanlee97.github.io

Figure-10: imaddabbura.github.io

Figure-11: www.eng.auburn.edu