Convolutional Neural Networks for Deep Learning

The method of convolution operation and its use for Deep learning.

This article is written as part of my course notes. It is written with a  view to make it useful for newcomers to the field as well as those with prior knowledge in related areas. Care is taken to minimize the mathematical rigor without losing the essentials. Machine learning and Deep learning is an area where programmers  exploit the easy-to-use APIs without being aware of the mathematics that works behind scenes. They can assemble such APIs to achieve good results. It is essential they realize that complex mathematical techniques are required to make most of the algorithms work. Mathematics is the driving engine for AI and ML algorithms.

Meaning of Convolution.

The literal meaning of the word to convolve is to twist, writhe or roll together.

A short quick look into the development of Convolution as a mathematical operation.

The story of mathematical operation of convolution started in 1760s when Swiss mathematician Euler introduced its theory in its more general form and linked it to the theory of differential equations involving continuous signals and functions. In the 19th and 20th centuries, it got extended to the theory of integral equations. The theories of differential equations and integral equations were born almost at the same time and may be considered twins. French mathematician Poisson used continuous convolution for many his studies and published his 1826 memoir about magnetism in movement. The earliest study of convolution for discrete (real or complex valued) functions and sequences of a set of integers for e.g., -∞ ≤ t ≤ ∞ was published by contemporary Frenchman Cauchy in 1821. These developments eventually led to the development of integral transforms like the Fourier and Laplace transforms. which play important roles to solve linear differential equations of physical systems by the applied mathematics and engineering community.

Concept of convolution as a computational method.

In mathematics convolution is an operation between two functions on a set, e.g., f(x) and h(x) is performed by reversing one and shifting it over the other. This results in a third function g(x). The term convolution refers to both the process of computing it and to the resulting output. Computing the inverse of convolution operation is known as deconvolution.  The operation denoted by ‘⁎’ that results in the third function g(x) expresses how the shape of one is modified by the other and is commutative. The symbol ‘⁎’ does not indicate a multiplication operation.

Convolution takes two functions and produces a third function. In signal processing these functions take the form of signals dependent on the independent variable ‘x’ (an example is time, x = t). Convolution describes the output (in terms of the inputs) of an important class of operations which are linear and time-invariant (LTI). For linear systems convolution is used to describe the relationship between an input signal f(x), transfer function of the system h(x) and its output signal g(x). If the system behavior characterized by the function h(x) is a unit impulse (delta function) then the resulting function (response) is same as the input signal, i.e., f(x) = g(x). If otherwise when the input signal f(x) is unit impulse function (delta function) then output signal is same as the system transfer function i.e., h(x) = g(x). Then it describes the characteristic behavior of the system which is called the impulse response of the linear system.

Figure - 1 

If the above system is a filter, then the impulse response being same as the transfer function is also called the filter kernel or the convolution filter. In image processing the filter kernel is also called the point spread function. Thus, convolution finds application in the design and implementation of impulse response filters (finite) in various signal and image processing applications. Convolution is the most important mathematical operation is signal processing. (To those readers not so familiar with Signal Processing or Linear system theory, I would request not to get stuck at this point but continue to read on.) 

The response of causal system must also be causal. A linear time invariant system is causal if its output f(t)∗ h(t) = g(t) depends only on present and past, but not future inputs. This means g(t) = 0 when t ≤ 0. This also means the system must not produce any output before the input signal is applied. The output is the convolution of the input signal with the impulse response of the system. For this to be true convolution must preserve causality. 

Convolution in the time domain is equivalent to multiplication in the frequency domain. Transformation from time domain to frequency domain can be performed by Fourier transform method. 

Reason to flip any one signal

Flipping makes sense since the inverse Fourier transform of the output resulting from convolution operation is same as the input convolved with the flipped impulse response. 

For arrays and matrices convolution performs a weighted sum of a collection of neighbouring elements of an array (or matrix). The weights used in the weighted sum calculation are also defined by an input array, commonly referred to as the kernel, filter or mask of the convolution. The kernel is usually shorter than the input signal.

The Fourier transform of convolution between two signals is the product of Fourier transforms of the individual functions. For linear systems whose characteristics do not change over time (LTI), the inverse Fourier transform of the response function equals the convolution operation with one signal flipped in the time domain, therefore flipping is required in the Fourier transform sense

Convolution of 1D signals illustrated in figures

The following figures illustrates the concept with both continuous and discrete signals

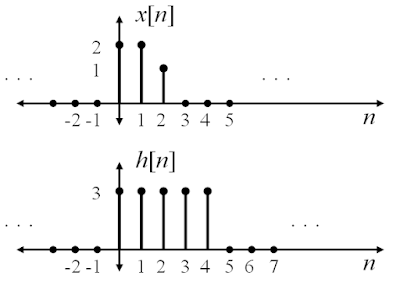
 Discrete case with two finite sequences of time instants (n).

When discrete then the operation is to "sum" the products between corresponding values with one reversed. 

Assuming x(n) and h(n) are discrete functions of time the mathematical expression is as follows.

 

To find     

 Consider the following signals

Figure - 2

 The following steps are performed.

 Step-1

Write both signals as functions of index “i”

 Step-2

Flip x[i] along y-axis to x[-i] . We flip x[i] since it is shorter. 

Figure - 3

 The following steps are performed for all values of n starting with n = 0

 The figures illustrate the steps only for a sample shifts at n = 0,.., 3,….,7.

Consider case n = 0, at n = 0 there is no shift. 

Step-3

 Figure - 4

Step-4

Compute the products h[i] ×x[i] for all values of “i” and sum the values over “i” to get y[0] = 6. 

Figure - 5

Case when x is shifted to n = 2,

The steps 3 and 4 is repeated, consider the shift n = 2,

 Step-3

Figure - 6

Step-4

Compute the products h[i] ×x[i] for all values of “i”

Figure - 7

Summation of these values over “i” will result in y[2] = 15.

Case when x is shifted to n = 7,

Steps 3 & 4 are continued until n = 6, at n = 7 there is no overlap between the two signals as shown in figure below.

Figure-8

Therefore convolution operation results in signal y[n] as shown. The signal y[n] is the output from the linear system with impulse response h[n] to an input signal x[n].

Figure - 9

 Continuous case with two signal functions of time (t).

When the functions f(x) and h(x) are continuous the operation "integrates" the product of the functions with one reflected with respect to the y axis. The resulting function is evaluated for all values of shift along the x-axis to produce the convolved output. 

The method is exactly same as the discrete case except that the discrete time index “n” is replaced by continuous valued variable e.g., time “t”. We flip h(t) since it is shorter. At Step-1 the functions are represented with independent variable “τ”. Steps-2, 3 and 4 are performed as for the discrete case variable. The function h(t - τ ) is shifted where “t” is shifted along the “τ”- axis. The linear system has an impulse response h(t) and convolving it with the input signal x(t) results in y(t) as shown in figure. 

Figure - 10

 The mathematical expression of the operation with x(t) and h(t) is as follows

 

If both functions are supported only in the region [0, ∞), then the expression can be modified as

If the two continuous functions are compactly supported then their convolution exists and is also compactly supported and continuous. A function has compact support if its value is zero outside the compact set. The following figures illustrate the concepts of support and compactness.

 Compact set

A set S or real numbers is compact if every sequence in S has a subset that converges to an element contained in S itself.

Figure - 11

 Support of a function f(.)

 A function “f(.) ” if real valued function with domain Ω = Rⁿ, the support of f(x) is the smallest closed set of K (subset of Rⁿ) such that f(x) = 0 for all x not belonging to K.

Figure - 12

Convolution between 1D arrays

 Notice that computations for y[2] are performed with the kernel w[n] flipped.  

1D Convolution

Figure – 13

Convolution and Cross-Correlation

Cross-correlation is a measure of similarity between two signal functions. The similarity measure over the entire function can be determined by moving the shorter one relative to the other along its independence axis or axes. For real-valued functions of continuous or discrete variables, certain features of convolution are similar to cross-correlation.

Convolution differs from cross-correlation only in that either h(x) or  f(x) is reflected about y-axis. Thus, it is a cross-correlation of h(x) and f(−x), or f(x) and h(-x), i.e. anyone of them flipped. For complex-valued functions, cross-correlation operator is the adjoint of convolution operator.

Convolution is a linear operation which results in a signal which is filtered by the filter kernel. If the filter kernel is symmetrical then there is no difference between the correlation and convolution operations. 

It can be seen that the product (continuous case) or sum (discrete case) of the two functions and hence value of convolution operation is maximum when the functions are similar and they overlap fully. When the functions do not overlap at all the product or sum is zero.

Commutative property of convolution.

Convolution is a commutative operation, and the commutative property is satisfied due to the flipping of the kernel with respect to input signal. Flipping is useful so that when the index increases, the kernel moves into the input while the index into the kernel decreases.

Consider a 2D image represented by I and the 2D kernel represented by K which are indexed by “m” and “n”.

Convolution between 2D arrays

In the following figures convolution operations are shown without flipping

The input is 3 × 4 matrix and the filter kernel is 2 × 2 matrix.

Figure - 14

The output results in another matrix of size 2 × 3.

A numerical example

Correlation with convolution kernel

Figure – 15

Figure-15 illustrates convolution of 3 × 3 arrays with a filter and its results. It is seen that the magnitude of the result increase the input array is more similar to the filter and reduces vice-versa when they are dissimilar.

Further illustrations of the use convolution for image processing

Edge Detection

Figure – 16

Shifting

Figure – 17 

Convolution in 3D illustrated with 3D tensors

Convolutional layers in 3D have a three-dimensional volumetric information. The depth of the convolutional layers will depend on the number of filters. Three dimensional filters have width, height and depth.

Applying volumetric filters for RGB images.

Figure - 18

Convolution for ANNs

The commutative property is not important for ANNs. Hence in most applications for ANNs convolution and cross-correlation is same and flipping is not required. The learning algorithm will learn the appropriate values of the kernel in the appropriated places as the kernel is shifted along the input.  

Convolutional Neural Networks (CNN) a short history

Inspired by the study of human visual system by Hubel and Wiesel in 1962, K. Fukushima introduced his Neocognitron in 1979 is a hierarchical multilayered network  which has the so called S-cell and C-cell layers that are alternating cells. These networks were specifically developed to solve computer vision related pattern recognition problems.  Fukushima’s Neocognitron served as predecessor to CNNs. The S-cells and C-cells were similar to the convolutional and pooling layers used in CNNs.

In 1989 Yann LeCun of Bell labs combined the ideas of convolutional neural nets and backpropagation algorithm for handwritten digit recognition. These networks could be trained to recognize image patterns recognition from raw pixels. These networks later came to be known as Lenet-5 used by US postal department to read ZIP codes.

In 2006 Chellapillai and his group followed by Yoshua Bengio and his team 2007 effectively used GPUs to train CNNs.

In 2012 Alex Krizhevsky from Geoffrey Hinton lab at University of Toronto pioneered a deep learning architecture (currently called Alexnet) with convolution. This convolutional neural network architecture won the computer vision competition (ImageNet challenge) by reducing the error rate by 26.1%. Later developments that followed were VGGNet by Simonian and Zisserman in 2014, GoogleNet by Szegedy et al., in 2015, ZFNet (Zeiler and Fergus 2015) and ResNet by He et al., in 2016 and more.

Convolution plays important role in digital audio, image and video signal processing. Graphics Processing Unit (GPU) hardware used to accelerate deep learning are optimized to execute convolutions. 

Limitations of feature selection by classical Machine Learning methods

Consider a computer vision problem such as human face recognition. To recognize human face under various conditions such as lighting variations, partial occlusions, cartoons, crumbled images, various orientations, color differences, etc., would require thousands of features. For machine learning algorithm to be efficient and fast we will need to train it with large datasets. It needs careful selection extraction of useful features from a large dimensional feature space to produce a lower dimensional representation. Appropriate feature selection is by itself a complex and tedious task. Human brains can perform such tasks with ease and high efficiency. This means our brain performs such tasks at a high level of feature abstraction that can well represent the higher dimensional data at lower dimensions. Before the introduction of deep learning algorithms for computer vision and machine learning, researchers needed a lot time and effort to select the most appropriate features to achieve reasonably high accuracy for image recognition tasks. 

Vanilla Deep Neural Networks for feature selection and learning

Deep learning architectures could learn to select appropriate features from a sufficiently large dataset. The simplest approach would be to use a vanilla (which means a standard fully connected with back propagation) architecture that will need a large number of weight parameters to recognize images for a full-color image of even size 200 × 200 pixels.  For multiple layers and larger images the total number of parameters for full connectivity would scale up very quickly, leading to expensive compute and training time and even overfit on training data.

Convolutional Neural Networks (convnets)

Many of these problems can be minimized with CNNs. CNNs are a type of hierarchical feedforward networks, where invariance to certain transformations of the inputs are built into the structure of a neural network. CNNs makes use of local receptive fields and shared weights. They are being widely applied to image and speech data. This network can be sparse, such that all possible connections between the layers being not be present. CNNs are robust against transformation due to translation, scaling, orientation and elastic deformation of features.

Major object detection models and architectures like You Only Look Once (Yolo), Single shot Detection (SSD), RCNN, Fast RCNN and Faster RCNN by Girshick, Shaoqing Ren, Kaiming He and Jian Sun in 2015 use CNNs.

Motivation from the neuroscience of primary visual cortex

The mammalian brain performs millions of convolutions per second on the sound, light and other sensory signal received from the external world.

Convolution in 2D illustrated with matrices

Human visual pathways

Figure – 19

Hierarchy in the organization of brain networks

Convolutional Neural Networks are inspired from biology. The cells within the biological visual cortex are sensitive to small sub-regions of the input space, called receptive fields, the region of the retina where the light falls. The receptive field of an individual sensory neuron is the particular region of the sensory space (e.g., the body surface, or the visual field) in which a stimulus will modify the firing of that neuron.  It is tiled in such a way as to cover the entire sensory (visual) field. They are usually considered two dimensional with circular, square or rectangular shapes. 

Hierarchical Structure

Figure - 20

The lateral geniculate nucleus (LGN) in thalamus receives its input from the retina and transmits retinopathic information from both eyes through optical nerves to occipital region in primary visual cortex. The information from LGNs makes it easy for primary visual cortex also called V1, to combine inputs from both eyes. The visual cortical system has a hierarchical structure to process the visual input signal sensed by the retina. Receptive fields act like local filters of the input space and are thus better suited to exploit the strong spatially local correlation present in the input space.

The term receptive field is also used in relation to  CNNs.  CNNs are designed to mimic the way in which real animal brains are understood to function. Instead of having every neuron in each layer connect to all neurons in the next layer, with CNNs neurons are arranged as a 3-dimensional structure in such a way as to take into account the spatial relationships between different neurons with respect to the original data.

NETWORKS WITH WEIGHT SHARING

In many applications of pattern recognition, it is known that predictions should be unchanged, or invariant, under one or more transformations of the input variables. For example, in the classification of objects in two-dimensional images, such as handwritten digits, a particular object should be assigned the same classification within the image irrespective of its

 Position(translation invariance) or

1. Size (scale invariance) and
2. Elastic deformation (warping).
3. Orientation (rotational invariance).

One way to deal with such data is to extract features that are invariant to above types of input data. For images such transformations in the input expressed in terms of the intensities at each of the pixels in the image should give rise to the same output from the classification system.

Example of image with scale change and elastic deformation 

Figure - 21 

Similarly speech is temporally ordered signal. It can undergo various levels of nonlinear warping along the time axis. Speech patterns should be recognized such that it should not change the interpretation of the signal.

If sufficiently large numbers of training patterns are available, then an adaptive model such as a vanilla neural network can learn to be invariant for all transformations of data from the same class, at least approximately. In most cases it is impractical to have a large training set. We therefore seek alternative approaches to develop an adaptive model that exhibits the required invariances. These can broadly be divided into following categories:

1. The training set is augmented using replicas of the training patterns, transformed according to the desired variances.
2. A regularization term is added to the error function that penalizes changes in the model output when the input is transformed.
3. Invariance is built into the pre-processing by extracting features that are invariant under the required transformations. 

The final option is to build the invariance properties into the structure of a neural network (or into the definition of a kernel function in the case of techniques such as the relevance vector machine).

Invariance property of CNNs

Consider the case of hand written digit recognition. The identity of the digit must be invariant under various tranformations. This invariance property can be built into the convolutional neural networks by selecting small subregions of an image. This image patch can be used to extract local features through three mechanisms:

(i)        local receptive fields,

(ii)       weight sharing, and

(iii)      pooling.

Architecture of 1d CNNs

Figure shows the architecture of convolutional 3-layered neural network to perform convolution on a one-dimensional array of inputs. Each convolutional layer has a layer of filter kernels to produce corresponding feature maps which are then connected to the next layer.

In the following figure the first layer is indicated by (m-1) layer. The (m-1) layer has spatially contiguous receptive fields of width 3. The second layer units in the m^th layer are connected to local subsets of units (3 contiguous units) in the (m-1)^th layer. Each unit in the m^th layer are at delayed locations (shifted to the right) and can accept simultaneously receive 3-inputs from the (m-1)^th layer units. The selection window is shifted at discrete intervals. These shifts correspond to delays in spatial locations as well as in time. The units in the (m+1)^th layer also has a receptive field of width 3 with respect to the m^th layer below, but their receptive field with respect to the input (m-1) is larger (it is 5).

Hierarchical layers

Figure – 22

These units in a layer act like “filters” to produce the strongest response to a certain feature from its  receptive field below and are unresponsive to variations outside of its receptive field. The architecture thus confines the units in any layer “m” to correspond to a spatially local feature and performs feature extraction from its previous layer.

Shared Weights /Filter Kernels and feature maps (for illustrations see 2D)

 

At any layer “m” the number of kernels will decide the depth of feature maps. These kernels are connected to small local regions of the previous layer, thus reducing number weight parameters compared to fully connected architectures. Viola and Jones in their IEEE paper published in 2001 had partially demonstrated this concept.

 

At any m^th layer the individual neuron units corresponding to delay is constrained to have the same values when shifted from right or left. Any m^th layer will comprise of multiple feature maps (Figure shows only one feature map).  Each neuron unit in a feature map is responsive only to a specific feature. The m^th layer thus forms a computational layer capable of mapping multiple features from the previous layer. The following figure shows 3 hidden nodes belonging to the same feature map at layer m.                     

Weight sharing

Figure - 23

Weights of the same colour are shared which means they are constrained to be identical. Replicating units and sharing the weights in this way, allows for specific features to be detected regardless of their position in the visual field. This method of weight sharing greatly reduces the number of free parameters to learn.

 

The units in the m^th layer perform like sparse filters that are replicated across the entire input field from the (m-1)^th layer. These “replicated” units which share the same parametrization (the same weight vector and the same bias) form a feature map,

 

Due to this weight sharing and sliding, the evaluation of the activations of units in the hidden layer “m” is equivalent to a convolution of the outputs from its previous layer units with a ‘kernel’ comprising the weight parameters. Hence the network is called convolutional neural network.

 
Benefits

This sharing of weight values has the following benefits.

1. The number of free parameters are reduced.
2. Shift invariance can be built into the feature maps.

Influence of the shift (strides) of filter kernel and number of feature maps

As the stride or shift length increases the number of feature map nodes at layer “m” decreases

 

Feature maps at (m-1)th and m^th layer

 

Figure - 24

Output node size equation

For a input of size i, a kernel size of  “k”, padding size “p” and stride size “s”, the output size o is given by

For 2D applications the above equation is applied along the rows and columns.

Padding

Padding is often required on either side of the input array in CNNs. It refers to the number of elements added on sides of the array so that the input array is fully covered by the kernel size and the stride size. For the above figure p = 0.  Keras provides options for padding

 1) “same”, this means input data is padded with zeros on either sides or the array such that  the output size of feature map form the layer is exactly same as the size of the input data, if s = 1. The input data is extended so that the kernel covers the entire input while it is shifted

2) “valid”, this means the dimensions of the input is valid and hence retained, i.e., no padding done.

3) “causal”, zero padding is done only at start of the input array

Sparse interactions in CNNs (Convolution matrix and sparsity)

For a fully connect neural network interaction each unit in a given layer is connected with every unit of its previous layer which forms its input layer. Convolution networks have sparse connectivity or sparse weights which is accomplished by making the kernel matrix much smaller that the input matrix.  In addition to the above constraint, convolution matrix is also constrained to be sparse matrices (matrices with most entries equal to zero).

Activation functions of Convolution Layer

Nonlinearity of convolution units are introduced by ReLU, sigmoid and tanh functions. The use of ReLU for training CNNs (Nair and Hinton, 2010) speeds up training.

Pooling (for illustrations see 2D)

A convolutional layer is followed by a computational layer that performs either of the following

1. Subsampling
2. a) Average pooling (local averaging), b) Global average pooling
3. Max pooling layer.

These operations further reduces the sensitivity of the feature maps output to translation, scaling, orientation, elastic deformation and reduces overfitting.

Final layer to the output units

 

The final layer is a dense layer or fully connected with softmax activated output units. The input from the previous hidden pooling or convolutional layer is flattened and converted to a one-dimensional array representing a feature vector of the input data. This feature vector is fed to the fully connected layer and transformed into outputs. The number of output nodes depends on the number of classifications required. The softmax activation units at the output function assigns probability values for each class 

1D Convnet

Figure - 25

Architecture of 2D and 3D CNNs - application to images

Convolutional networks were specifically designed to recognize 2-D shapes with a high degree of invariance to translation, scaling, warping and orientation. An image comprises a set of pixel intensity values. A key property of images is that nearby pixels are more strongly correlated than more distant pixels. This property can be exploited for extracting local features that depend only on small subregions of the image. Information from such features can then be merged in later stages of processing in order to detect higher-order features and ultimately to yield information about the image as whole. Also, local features that are useful in one region of the image are likely to be useful in other regions of the image, as in case objects of interest that are translated or shifted in location. 

The structure of a 2D convolutional network is illustrated in Figure. It shows the architectural layout of the convolutional network for character recognition. The network is made of an input layer, hidden layers and output layer. 

2D - Convnet

Figure - 26 

As an example, let the input layer be made up of 110 x 110 sensory nodes. It receives images of different characters that are approximately centered and normalized. The first hidden layer performs convolution on input layer. Convolutional layers are organized into planes, each of which is called a feature map. Each neuron unit in a feature map is assigned with a small subregion of the image (e.g. 5× 5 pixel patch of the image). This pixel patch is known as the local receptive field.  Individual neuron units connected to the local receptive fields, in a feature map are constrained to share the same set of weight values. In the example shown below the feature map shown in figure consists of 100 units arranged in a 10 × 10 grid.

The synaptic weights are trained using back-propagation algorithm. It is also possible to incorporate prior knowledge into the weight values about the task at hand.

The convolution on layer (m-1) is followed by a subsampling layer that performs subsampling and local averaging, whereby the resolution of the feature map is reduced. This reduces the sensitivity of the feature maps outputs to shifts and other forms of distortions. The output layer performs the final stage of convolution. 

Alternating layers of convolution and pooling

Figure - 27 

Weight matrices for feature maps

Figure - 28 

Figure shows two layers of a CNN, containing 4 feature maps at layer (m-1)⁰, (m-1)¹, (m-1)² and (m-1)³ at layer (m-1) and 2 feature maps (m⁰ and m¹) at layer m. At layer m, pixels (neuron outputs) in m⁰ and m¹ (outlined as blue and red squares) are computed from the pixels of layer (m-1) which fall within their 2 x 2 receptive field (shown as colored rectangles). These receptive field spans four input feature maps of (m-1) layer. The weights matrices W⁰and W¹of m⁰ and m¹ are thus 3D weight tensors. 

Figure -  29 

A feature map of an image is obtained by convolution with a filter kernel that is moved across the entire image. As the number of feature maps increases and with increasing depth of convolutional layers the model complexity increases causing heavy computational burden especially during training. Consider as an example a image 96 × 96 pixels with 400 convolutional filters of 8 × 8 pixels for first hidden layer. With stride s = 1 and padding p = 0, each feature map will have (96-8+1)² = 7921 feature nodes. For 400 filters there will be 3,168,400 hidden nodes with trainable synapses. 

ages is that neighbouring pixels are highly correlated and some features in one area can be useful also for another area. Therefore, aggregation statistics (mean, variance, etc.) can be used at different locations. These statistical features can reduce feature dimensionality. This method of reducing feature dimensionality is called pooling. Each convolutional layer is followed by a computational layer that performs pooling. The following methods can be used.. 

Subsampling (Downsampling) 

Figure - 30

 Average pooling (local averaging), 

Figure - 31 

Global average pooling 

Figure - 32 

Max pooling layer (not shown in above figures, see figures for 2-D). 

Figure - 33 

An important concept of CNNs is that of max-pooling, which is a form of non-linear sub-sampling. Max-pooling partitions the input image into a set of non-overlapping rectangles and for each such sub-region outputs the maximum value. Max-pooling is useful in vision for two reasons:

(1) it reduces the computational complexity for upper layers and

(2) it provides a form of translation invariance.

To understand that it provides translational invariance, imagine cascading a max-pooling layer with a subsequent convolutional layer. There are 8 directions in which one can translate the input image by a single pixel. If max-pooling is done over a 2x2 region, 3 out of these 8 possible configurations will produce exactly the same output at the convolutional layer. For max-pooling over a 3x3 window, this jumps to 5/8.Since it provides additional robustness to position, max-pooling is thus a “smart” way of reducing the dimensionality of intermediate representations.

Sample architecture of CNN

Figure-34

Training

 

The standard back propagation algorithm can be used for training the network. Back propagation uses error gradients to update the weight values of every synapse.  The magnitude of the weight updates depends on the learning rate, input value and the error gradient. For more details on BP training and gradient descent method read the corresponding article on these topics in the same blog site. The method works properly when the weight update values are small and controlled. During training the gradients from the deeper layers undergo matrix multiplications due to the chain rule. This can cause the vanishing gradients when gradient values are < 1. 

When gradient values are > 1, it causes the exploding gradient problem. The network will crash due to value overflow of its activations. These problems are severe for very deep networks and vanilla recurrent neural networks, and so on.    

   

Vanishing gradient

 

The gradients of logistic sigmoid and tanh functions tends to become zero when the unit activation values are large in magnitude. This can cause the vanishing gradient problem in deep neural networks and simple recurrent neural networks. The network training ceases to learn. (For more detailed comparisons between various activation functions you may read the post on “Activation functions for Deep Learning” in the same blog series. The ReLU activation function can eliminate this problem in CNNs. 

The problem for deep neural networks was studied by Hoechreiter, Schmidhuber and Bengio in early 1990s. In 1997 Hoechreiter and Schmidhubher introduced Long Short Term Memory networks and in 2014 Kyunghyun Cho et.al. introduced the Gated Recurrent unit networks for RNNs to solve this problem. Layerwise training which means one layer at a time can also solve this issue for deep networks.

 

Exploding gradients

 

Because the input values are scaled and normalized generally to be within [-1, 1] and the weight values are also randomly initially to such similar range, it is not reasonable to assume that the weight values of hidden layers similarly scaled. In deep neural networks this problem occurs if gradient values are large,  the magnitude of the weight updates keeps increasing. Due to repeated multiplication of gradients the numerical values of weight updates can overflow and resulting in NaN. 

While back propagating the error gradient calculation of weight updates in earlier layers can become exponentially large causing wild fluctuations in the weight values. This makes training unstable. This is problem severely affects especially recurrent neural networks. It is essential to keep these values within a certain range. Some methods that can be adopted as gradient clipping and batch normalization. The following methods can be used to mitigate this problem.

 

Gradient clipping can be used to prevent the gradients magnitudes to exceed the threshold limits set. It is also good practice to check the gradient magnitudes intermittently to monitor the performance of training.  Keras provides two options clipnorm and clipvalues for gradient clipping. When clipnorm = 1, the gradients are ensured to be within  [-1, 1].

 

Batch normalization is another method. A batch normalizing layer is included after convolution layers or dense layers to normalize the outputs from these layers. This layer computes the mean and standard deviation of the layer inputs across batches of training data. The mean is subtracted, and the results are divided by the standard deviation.

Keras provides two learnable parameters (shift) beta and (scale) gamma for configuring batch normalization layers. The output from the batch layer are the normalized values shifted by beta and scaled by gamma.    During training Keras stores the moving mean and standard deviation for input data channel. During testing appropriate corrections are made at every layer.

Weight Regularization also called weight decay is used to prevent overfitting. Instead, regularization has an influence on the scale of weights, and thereby on the effective learning rate. The effect combining regularizing with normalization can be studied.

Effect of network complexity: Under-fitting, Over-fitting and the Bias/Variance Trade-off, Generalization vs Optimization capability

During training the network model tries to optimize its performance by minimizing the loss function. The network complexity increases as the number of layers and number of nodes per layer increases. A deep network with large number layer with many nodes has higher learning capacity than a shallower model and lesser number of nodes per layer. A model with more than sufficient capacity tends to overfit on the training data and vice-versa.

A network which is too closely fitted to the training data will tend to have low bias but a large variance. The model has optimized exceedingly on the data and memorizes even the noise present. We then say that over-fitting of the training data has occurred. The network which has highly optimized on the training on the training will have poor generalization capability. This means its performance during testing with unseen data will also be poor. (Article of various types optimizers available will follow later.) 

Variance can be minimized by smoothing the network outputs, but if this is taken too far results in high value of bias, and the generalization error is large again. We then say that under-fitting of the training data has occurred.  A network that has not learned to adapt will be underfit and have high bias but low variance. 

This trade-off between underfit and overfit plays a crucial role in the application of neural network techniques and learning algorithms to practical applications. There is always a trade-off between these conflicting requirements. Unfortunately, there are no straight forward techniques to strike a balance between the two.    The model designer may consider a grid of different architectures of varying complexity to find the most appropriate model for the data. A general method is to use the principle of “Occam’s razor”, which says given two explanations on something or two competing models, the simpler one is likely to be correct. The designer starts with a simple model with relatively lesser number of layers and parameters and increase them until he arrives at a point of diminishing returns for the available data. The following figure shows how the underfit error (approximation error) and overfit error (estimation error) varies as the model complexity “F” is increased. The idea is to choose the complexity level which the total error also called risk. This method of arriving at the minimum value of the risk functional or the best generalization performance by control variable “F” is called the method of structural risk minimization. 

Figure - 35

Figure - 36 

Dropout layer method in DNNs

There are many ways to reduce overfitting in machine learning algorithms. G. Hinton introduced the idea of using dropout layers in deep networks in 2012, which was presented in 2014 by N. Srivastava. While training a neuron output is active only with a certain probability “p”. During training each dropout layer chooses a set of random units with probability “1-p” and set their outputs to zero and the synaptic weights are not updated.  If dropout layers are uniformly spread across the whole network, overfit will be reduced and the model’s generalization performance on unseen data is improved. At test time the dropout layer does not drop any unit and the full network is used during testing, this is called inverted dropout.

Weight Regularization method to reduce overfit

Another way to mitigating overfit is to make the weight value more regular by taking smaller values. An extra cost associated with larger weight values is added to the loss function. This method penalizes the network when weight values become more irregular and the method is called weight regularization. Some examples are L₁ regularization, L₂ regularization and L₁ - L₂ regularization, etc.  (Article on various types regularizers will follow later.)

Pretrained Convnets and Transfer Learning.

Pretrained networks are saved models that were trained effectively on a large benchmark datasets of generic nature related to a problem domain e.g., image recognition, classification, audio and speech recognition etc. They can be serve as starting models and will minimize development time for new applications and solving problems with similar datasets. Using a pretrained network for new application and tasks is typically much faster and easier than training a network from scratch. The method is called transfer learning. 

Transfer Learning for classification

Figure - 37

The most important characteristics pre-trained networks are accuracy, speed, and size. Choosing a network is generally a tradeoff between these characteristics. (mathworks). The first of these type of networks was VGG16 which was later followed by modifications. Majority of these networks are pretrained on ImageNet database which is used in the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC). These networks have been trained on more than a million images and can classify images into 1000 object categories, such as keyboard, coffee mug, pencil, and many animals.

A few examples of various types of pre-trained networks are shown below 

Comparison of various pre-trained networks

Figure - 38 

A few applications of CNNs

1.     Acoustic modelling

2.     Automatic speech recognition

3.     Emotion recognition from speech

4.     Optical character recognition,

5.     Automatic text recognition.

6.     Face recognition

7.     Person detection

8.     Scene labelling and classification

9.     Object detection and segmenting

10.  Object tracking in video

11.   many more,

Other applications include solving differential equations in engineering, probability, statistics, natural language processing, etc.

 

References 

1. Kevin P. Murphy, Machine learning : a probabilistic perspective, MIT Press, 2012
2. Christopher Bishop, Pattern Recognition and Machine Learning, 2^nd Edition
3. Ian Goodfellow, Yoshua Bengio, Aaron Courville, Francis Bach, “Deep Learning”, MIT Press, 2016
4. Francois Chollet, “Deep Learning with Python”, Manning Publication, 2018,
5. David Foster, “Generative Deep Learning”, O’Reilly, 2019.
6. Nikhil Buduma, “Fundamentals of Deep Learning”, O’Reilly, 2019.
7. Claus C. Hilgetag and Alexandros Goulas, “Hierarchy’ in the organization of brain networks, ”  Philos Trans R Soc Lond B Biol Sci. 2020 Apr 13; 375(1796): 20190319.

8. Alejandro Dominguez, “A History of the Convolution Operation”,    IEEE Pulse, IEEE Engineering in Medicine and Biology Society,  Jan/Feb 20
9. Dimitrios Marmanis, Mihai Datcu,  Thomas Esch, and Uwe Stilla, “Deep Learning Earth Observation Classification Using ImageNet Pretrained Networks” , IEEE GEOSCIENCE AND REMOTE SENSING LETTERS, VOL. 13, NO. 1, JANUARY 2016 105  
10. wikipedia.org
11. mathworks.com
12. mathworld.wolfram.com

 

Image Credits

Figures: 2 – 9 adapted from electricalacademia.edu.

Figure – 10: fourier.eng.hmc.edu

Figure – 12: researchgate.net

Figure – 13: researchgate.net

Figure – 14: Reference 3

Figure – 17: Fm.blog.naver.com

Figure – 18: stackoverflow.com

Figure – 19: www.researchgate.net

Figure – 25: media.springernature.com

Figure – 27: adapted from figure 30

Figure – 29: dlblogcom.files.wordpress.com/

Figure – 30: socs.binus.ac.id

Figure – 31: embarc.org

Figure – 32: peltarion.com

Figure – 33: cdn-images-1.medium.com

Figure – 34: web.stanford.edu

Figure – 35: jobilize.com

Figure – 36: youtube.com

Figure – 37: Reference 9

Figure – 38: mathworks.com